Cubo mágico

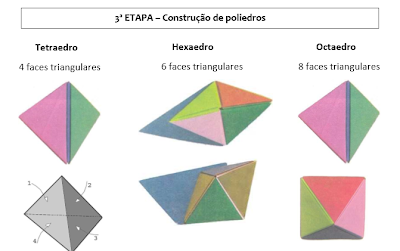
 O cubo mágico é um quebra cabeça que possui todas as características citadas. Ele é um jogo tridimensional composto de 6 faces de cores diferentes divididas cada uma em 9 partes de tamanhos iguais. As linhas e colunas devem ser giradas para que o cubo seja montado de forma que as faces possuam todas as partes de mesma cor.

Esse quebra cabeça é conhecido mundialmente e sua criação é atribuída ao húngaro Erno Rubik. Com base nesse cubo de dimensões 3 x 3 x 3, foram criado os cubos de dimensões 4 x 4 x 4 e 5 x 5 x 5. Veja:

. O brinquedo pedagógico estimula a participação, desinibindo os mais tímidos e promovendo uma maior interação social.

Tutorial

- Lista de algoritmos -

Cruz
1 - F U' R U (Inverter peça de meio)

Cantos da Primeira Camada
2 - R U R' (Colocar peça de canto quando na direita)
3 - L' U' L (Colocar peça de canto quando na esquerda)
4 - R U2 R' (Girar peça que esteja com adesivo branco para cima)

Segunda Camada
5 - U R U' R' U' F' U F (Colocar peça de meio quando para a direita)
6 - U' L U L'  U F U' F' (Colocar peça de meio quando para a esquerda)

Orientação dos Meios da Última Camada
7 - F U R U' R' F' (Ponto - Linha - 9 Horas - Cruz)

Orientação dos Cantos da Última Camada
8 - R U R' U R U2 R' (Peixe - Cruz, variado)

Permutação dos Cantos da Última Camada
9 - R' F R' B2 R F' R' B2 R2 (Colocar os cantos no lugar)

Permutação dos Meios dos Última Camada
10 - F2 U L R' F2 L' R U F2 (Gira os meios no sentido horário)
11 - F2 U' L R' F2 L' R U' F2 (Gira os meios no sentido anti-horário)

Quadrado mágico

Uma boa atividade para alunos de quinta série com números naturais e sétimo ano com números inteiros:

Quadrado Mágico 3 x 3 somente com números naturais .

    Quadrado     5 x 5  com números inteiros , podendo ser aplicado ao 7o ano , cujo a soma de todos os lados tem que ser 10.

Dobraduras de Poliedro

A seguir tutorial para montagem de diversos poliedros através de dobraduras de papel

  A seguir alguns poliedros montados por meus alunos de oitava série:

 Icosaedro - 20 lados triangulares iguais  personalizado  

Octaedro - 8 lados iguais

Tetraedro - 4 lados iguais

Desenhos no plano cartesiano

Esta é uma atividade muito interessante que pode ser aplicado aos alunos de sétimos e oitavos anos após o inicio de aprendizado das coordenadas de plano cartesiano . A seguir o link pra download  das demais propostas de desenhos misteriosos a partir da coordenadas extraídas do site neoparaiso.com

17 desenhos para confecção da atividade

Dificuldades na tabuada? Tabuando Legal

Esta é uma atividade muito importante , estimulante e interessante para alunos com dificuldades proposta pelo caderno de atividade de experiência matemática para a prática de tabuada o qual dois alunos desafiam um ao outro através da escolha de cartas numéricas, perguntas  decorrentes da tabuada , o qual a resposta será confirmada ou não por um terceiro aluno em posse e consulta da tabuada , dos valores corretos das respostas:

       TABUANDO  LEGAL

 Primeiramente os alunos que apresentam dificuldades similares, devem estar sentados um de frente ao outro acompanhados de um terceiro aluno (fiscal), que estará sob a consulta da tabuada para a conferência das respostas. O fiscal deverá anotar o nome dos dois alunos participantes do treino em desafio na seguinte tabela :

Após a escolha de quem inicia, os alunos deverão  escolher  e virar  sobre a mesa as cartelas numeradas, sendo alternadamente  uma por vez , e assim perguntar ao oponente um número qualquer da tabuada envolvendo a cartela numérica virada 

O aluno fiscal anotará um x na tabela correspondente ao nome do aluno que acertou a resposta , processo que poderá ser feito por uma ou diversas rodadas que presume-se de 1 a 10 perguntas cada rodada.

Porcentagens com o labirinto elétrico

Olá pessoal, a imagem a seguir mostra a foto de um labirinto elétrico que montei , mas com uma adaptação  diferente que foi o pequeno motor extraído do brinquedo de ventilador dos doces que vendem no supermercado.

 

  Objetivos ( treinar coordenação e principalmente porcentagens)

Perceba que pintei com guache a linha do carretel , foram 3 cores diferentes a cada 100 voltas ( azul , amarelo e preto)

Regras:

  1 - O aluno deve percorrer a haste com a argola envolto ao arame sem tocá-lo (ida e volta) , pois ao tocar o rotor do ventilador gira enrolando o carretel de linha na bucha . A a cada cor que aparecer na bucha 100 voltas foram dadas.

2 - Após o percurso total com a argola, o aluno saberá mediante a cor enrolada na bucha quantas voltas foram dadas de linha e tomará como padrão uma tabela para calculo :

     até cor azul                -     100
     entre azul e amarelo    -    200
     entre amarelo e preto  -    300
     após preto                  -    400

Exemplo :  Caso o aluno tenha em sua mal coordenação enrolado linha entre as cores preto e amarelo, ele teria que calcular   300 / 400  =  0,75 =  75 %  de perca de coordenação.

Portanto em concorrência com outros alunos , quanto menor o percentual , melhor a coordenação motora e assim o ganho do desafio perante os colegas.  Espero que tenham gostado. Abraços..

Atividade Dinâmica com frações

     Esta foi uma das atividades de dinâmica  o qual desenvolvi  e obtive um retorno muito bom por parte dos alunos que gostaram e participaram dos desafios propostos mostrados a seguir:

   1 - Após apito inicial , os alunos devem encher as bexigas até estourar, pois dentro delas contém um papel com uma  representação de fração o qual devem representar com líquidos nos copos;

 2 - Após o estouro os alunos devem colocar os copos plásticos na bandeja conforme representação da fração requerida que estava dentro da bexiga;

3 - Ganha em pontuação a disputa o aluno que primeiro colocar o total de copos na bandeja e encher conforme a representação , no caso da vencedora foi   5/8

Geométricos apenas com compasso

   Olá pessoal , através das rosáceas é possível a formação de grande parte das figuras geométricas planas somente com a utilização do compasso.

   Mas enfim o que são rosáceas?

A rosácea é um elemento arquitectónico ornamental usado no seu auge em catedrais durante o período gótico. Dentro do eixo condutor deste período artístico, a rosácea transmite, através da luz e da cor, o contato com a espiritualidade e a ascensão ao sagrado. (Wikipédia).

 Na construção da  rosácea é possível verificas que são círculos entre os centros que apresentam mesmo raio  de distâncias  o qual é possível a partir dos pontos de intersecção forma-se diversas figuras geométricas planas, portanto é possível a construção destas rosáceas utilizando um simples compasso com abertura fixa definida.

A seguir algumas construções de rosáceas prontas feita no software geogebra e figuras geométricas construídas  por alunos de sextos e sétimos anos  sobre elas:

Aplicação Teorema de Pitágoras

    ESTA É UMA ÓTIMA  APLICAÇÃO QUE DEMONSTRA O TEOREMA DE PITÁGORAS COM A UTILIZAÇÃO DE LÍQUIDOS , É POSSÍVEL VER QUE O VOLUME DOS LÍQUIDOS DOS CATETOS VAI ENCHER O QUADRADO DA HIPOTENUSA

Matemática em toda parte

MATEMÁTICA EM TODA PARTE Às vezes a matemática pode parecer uma coisa muito longe de nossa "vida real". Não é bem assim: a matemática é uma valiosa ferramenta para resolver problemas. Por meio dela, podemos não só encontrar uma solução como, pela sua lógica e precisão, estabelecer uma maneira de resolver problemas semelhantes. Cálculos matemáticos estão na base de tantas e tantas coisas que fazem parte do nosso cotidiano que é impossível relacionar tudo. Basta dizer que sem eles você nem teria esse computador diante dos olhos. Apesar de ser uma ciência milenar, a matemática está sempre em transformação, respondendo aos novos desafios, colaborando decisivamente para os avanços tecnológicos. Geralmente, divide-se a matemática em duas áreas: matemática pura e matemática aplicada. A matemática pura vai fundo na teoria, nas questões abstratas. Não é sua função se preocupar com a prática dos resultados. Os problemas práticos ficam por conta da matemática aplicada, capaz de encontrar soluções para as áreas mais diversas, como física, economia, navegação, etc.